SAM - 后缀自动机
问题引入
假如我们要用一个有向无环图存一个字符串的所有子串,然后跑各种图论中的算法,以 $abaab$ 为例,该怎么做
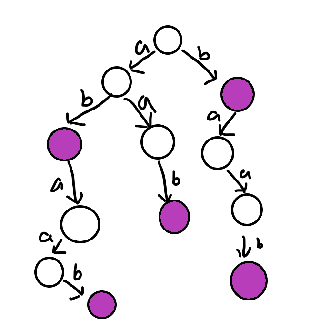
SAM介绍
注意到,这种方法的时间在最劣的情况下是 $O(n^2)$ 的,因为其中还有很多部分可以优化
观察到 $a→a→b$ 和 $a→b→a→a→b$ 这两条路可以优化至一条, 所以我们可以考虑一种数据结构存储一个字符串的所有字串并使其优化掉尽可能多的节点和边。
有了这个图处理许多事情。包括但不限于判断某一个串是否为原串的子串(从源点跑这个串,跑到空节点就说明不是子串)、不同子串个数(在 $DAG$ 上跑 $DP$ )等,在使用了后缀自动机后,功能还能多上许多。
根据上述问题的介绍,我们可以认为SAM是给定字符串的压缩形式。
对于一个长度为 $n$ 的字符串,SAM至多有 $2n-1$ 个节点和 $3n-4$ 条边。
分类:字符串/数据结构
而且构造SAM的时间复杂度和SAM的空间复杂度都是 $\text{O}(n)$ 的。这就是为什么SAM是高贵的线性算法
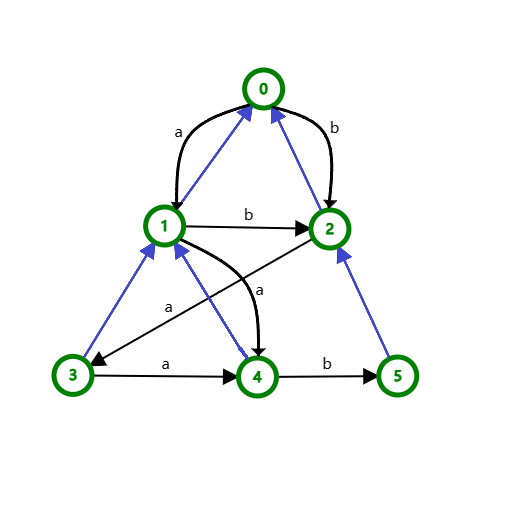
如右图,是字符串 $abaab$ 跑出来的SAM的结构
我们可以发现,SAM是一个数据结构——以一张DAG(有向无环图)为基础的储存字符串的信息的数据结构
其中,蓝色的边构成了一棵树,而黑色的边上存有一些字母,那他们的用处又是什么呢
SAM的构成
节点(状态)
上文中,我们已经了解了SAM是一个DAG,那么接下来我将讲述SAM中节点的作用以及含义
endpos
对于一个字符串 $S$,$endpos(s)$ 为 $s$ 在 $S$ 中所有出现的结束位置所构成的集合。
举个例子,当$S=“abaab”$ ,$endpos(ab)={2,5}$ ,$endpos(baab)={5}$ ,$endpos(a)={1,3,4}$ ,对于 $endpos$ 相同的子串,我们将它们归为一个 $endpos$ 等价类,比如 $abcabc$ 中 $“abc”$ 和 $“bc”$ 和 $“c”$ 的 $endpos$ 皆为 ${3,6}$ ,属于一个等价类 ,当$s_1,s_2$ 为 $S$ 的字串时,若 $|s_1|≤|s_2|$ 且 $endpos(s_2) \subseteq endpos(s_1)$ ,则 $s_1$ 为 $s_2$ 的后缀 SAM中的一个状态包含的子串都具有相同的endpos,那么他们互为后缀
以 $S=“abaab”$ 为例,$endpos(“ab”) = \{2,5\}$,$endpos(“aab”)=\{5\}$
所以 $ab$ 为 $aab$的后缀。
- 证明
$|s_1|≤|s_2|$这个条件是显然的
若 $endpos(s_2) \subseteq endpos(s_1)$ ,则 $s_2$ 结束的每一个位置,都是 $s_1$ 结束的位置,而 $s_2$ 的长度大于等于 $s_1$ ,所以 $s_1$ 肯定是 $s_2$ 的后缀,可证明充分性。
若 $s_1$ 是 $s_2$ 的后缀,则 $s_2$ 结束的位置 $s_1$ 也结束了一次,所以可证明其必要性
对于任意一个 $endpos$ 等价类,将包含在其中的所有子串依长度从大到小排序,则每一个子串的长度均为上一个子串的长度减 $1$ ,且为上面所有子串的后缀,换句话说,是上一个子串的真后缀
- 证明
为上面所有子串的后缀是显然的,可以通过之前提到的性质证明
尝试证明每一个子串为上一个串的长度减 $1$,考虑反证。
1. 第一种情况是它与上一个子串的长度相等,这是显然不可能的,因为它是上一个子串的后缀,而若长度相等,则它与上一个子串相等,就毫无意义了
2. 第二种情况是它为上一个子串的长度减 $x(x>1)$,在这种情况下,首先我们假设当前子串为 $s$,上一个子串为 $s_1$,存在 $s_2$ 为上一个子串的真后缀,根据上述性质,因为 $endpos(s1) \subseteq endpos(s_2)$ 且 $endpos(s_2) \subseteq endpos(s)$,又因为 $endpos(s) = endpos(s1)$ ,所以 $endpos(s_2) = endpos(s) = endpos(s_1)$
在知道了endpos是什么后,我们不难发现,SAM中的每一个节点就是一个endpos等价类
观察这个长度为 $n$ 的SAM(如上图)
注意到有初始状态 $t_0$(图中标号为 $0$ 的点),$t_0$ 具体为endpos等价类 ${1,2,3,4,...,n-1,n}$,以初始状态为起点,沿着字符转移(黑线)走,均能到达任意一个节点,且经过的字符组成的字符串是 $S$ 的子串。
也有终止状态,可以发现对于一个字符串的后缀,我们都可以从 $t_0$ 出发沿着字符标示的路径(黑线)转移至终止状态, 也就是说从源点到任意终止节点的任意路径形成的字符串均为原串后缀。
字符转移
注意到图中的黑边,它们是字符转移,将一个等价类中所有的子串后方加上字符转移所代表的字符,得到了若干新的子串,它们将转移至(来到)新的等价类,这就是字符转移
后缀链接
注意到,右图中存在一些蓝边, 他们是后缀链接(link),那后缀链接是什么呢?
由上文可以得知,SAM上的每一个节点都对应了一个 $endpos$ 等价类,例如右图 $abb$ 跑出来的的SAM。
对于一个 $endpos$ 等价类 $x$,我们将其中长度最长的字串设为 $longest(x)$,最短的子串为 $shortest(x)$。
比如 $endpos$ 等价类 $3$ 中有 ${abb,bb}$ ,其中 $longest(3) = “abb”$ 、 $shortest(3)=“bb”$
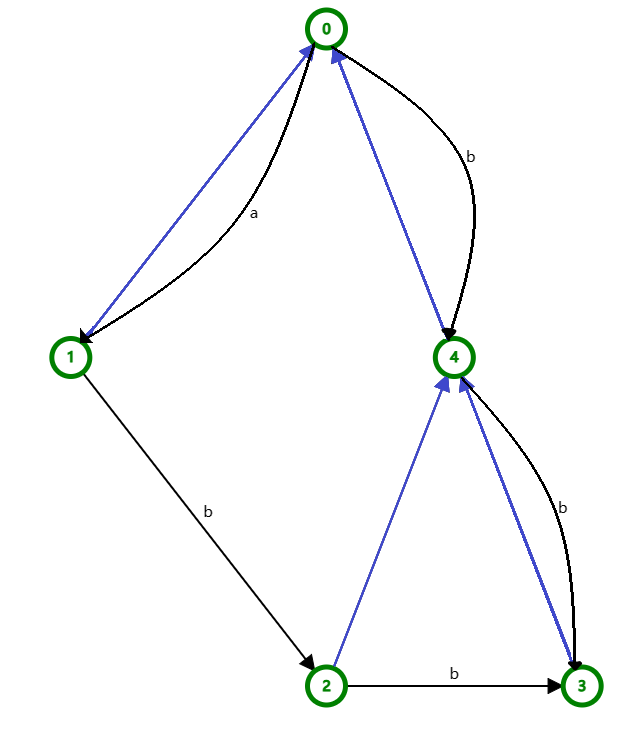
而后缀链接 $link(u)$ 则指向了 $v$ ,$v$ 代表 $shortest(u)$ 的最长真后缀所在的 $endpos$ 等价类,是不是听不懂,那就以右图中 $longest$ 为 $abb$ 的节点 $3$ 为例。
在字符串 $abb$ 中,子串及其 $endpos$ 分别为
| 子串 | endpos |
|---|---|
| abb | 3 |
| bb | 3 |
| ab | 2 |
| b | 2,3 |
| a | 1 |
| 1,2,3 |
注意到 $endpos$ 等价类 $3$ 中的节点包含了 $abb$ 和 $bb$,而 $shortest(3) = bb$
$bb$ 的最长真后缀为 $b$ ,所以 $link(3)$ 指向了 $endpos$ 等价类 ${2,3}$
你知道吗:最长真后缀可以想象为一个字符串去掉它的第一个字符所形成的字符串
注意力足够惊人的同学可以发现,后缀链接构成了一颗内向树,整个SAM是构成了一颗以link为边, $t_0$ 为根的树,这是显而易见的。可以说,SAM是由字符转移构成的DAG+由后缀链接构成的树
构建SAM
终于讲完了理论上的知识,现在可以开始进行实践了
那我们如何建图呢。
SAM是一个一个插入字符来建图的,我们假设现在插入字符 $x$
我们定义 $cur$ 为现在建的节点,也就是加完 $x$ 之后整个字符串所在的状态
$lst$ 为上一个建的节点,也是在添加 $x$ 之前整个字符串所在的状态
$sam[u].nxt[x]$ 为一条从 $u$ 出发,字符为 $x$ 的字符转移指向的节点 $v$,若无指向,则为 $0$
$sam[u].link$ 则为 $u$ 的后缀链接
$sam[u].len$ 为 $endpos$ 等价类 $u$ 的 $longest$ 的长度
初始化时,我们使初始状态 $t_0$ 的后缀链接为 $-1%$
void init() {
sam[0].link = -1;
}
之后一个一个的插入字符
void string_insert(string s) {
for (int i = 0; i < s.length(); i++) {
sam_insert(s[i] - 'a' + 1);
}
}
插入字符
在每一次 $add(x)$ 当中,我们加入一个字符时,$cur.len$ 为 $lst.len+1$,这是显而易见的,加入 $x$ 之后,串就变成了 $S+x$ ,这一步操作后显然会出现一些新的等价类( $endpos$ 包含的字符 $c$ 的位置,所以肯定会变化)我们称这个新的等价类为 $cur$ 。
为了找到他的后缀链接 $link$ 并且将其他的 $nxt$ 指向它,我们可以定义一个 $p = lst$,之后不断跳到 $link(p)$ 去寻找 $link(cur)$ 并且将 $p.nxt[x]$ 指向 $cur$
具体来说,如果 $p≠-1$ 且 $p.nxt[x]$ 为 $0$(未指向任何点)时,我们就将 $p.nxt[x]$ 指向 $cnt$ 且将 $p$ 赋值为 $link(p)$ 实现上跳的过程。
按照这个过程 $p$ 所跳到的(包括 $lst$ )一定是 $S$ (加入 $x$ 之前)的后缀,而这些后缀加入一个 $x$ 的 $endpos$ 就是 $cur$
如果因为 $p=-1$ 或 $p.nxt[x]$ 不为 $0$ 而寻找停止的话,我们就进行分类讨论,因为此时的后缀加上 $x$ 的 $endpos$ 并不为 $cur$ 且 $endpos(cur)⊂endpos(p+“x”)$,其($cur$)最短后缀的最长真后缀属于等价类 $p$,所以我们应该添加一条后缀链接link了
分类讨论具体如下
-
如果 $p=-1$ 时,说明添加前的 $S$ 没有 $x$ ,说明此字串的最短字串的最长真后缀为空串,此时 $link$ 应指向 $t_0$,则 $link(cur) = 0$
-
否则将 $q$ 定义为 $p.nxt[x]$,如果 $len(p)+1 = len(q)$ 的话,说明 $longest(p)$ 加上 $x$ 为 $longest(q)$ ,此时 $q$ 的 $longest$ 为 $cur$ 的 $shortest$ 的真后缀,所以直接连一条后缀链接从 $cur$ 至 $q$ ,也就是 $link(cur)= q$
否则我们就应该创建一个克隆状态$cl(clone)$,使其 $len(cl) = len(p)+1$,且将 $cl$ 的 $nxt$ 复制为 $q$ 的 $nxt$ ,并将 $cl$ 的 $link$ 指向 $q$ 的 $link$(相当于将 $q$ 的 $nxt$ 和 $link$ 赋给了 $cl$),之后继续让 $p$ 向 $link$ 找,并将 $sam[p].nxt[x] = clone$,直到 $p=-1$ 或 $sam[p].nxt[x] = q$,最后,将 $q$ 和 $cur$ 的 $link$ 指向 $cl$ ,至于原因,由于这是SAM构造中最难的部分,我们将另开一个块来讲
为什么我们需要克隆状态
注意力惊人的同学可以观察到,我们在添加一个 $x$ 构建新等价类的时候,容易出现让旧的等价类内出现 $endpos$ 不相等的可能
比如对于串 $caba$ ,旧的等价类($3$)里面有 $ab$,和 $cab$,现在我们在串 $caba$ 后面添加了一个 $b$ ,此时 $ab$ 的 $endpos$ 变为了 $(3,5)$ ,但 $cab$ 的 $endpos$ 还为 $(3)$,出现了一个等价类内 $endpos$ 不相同的情况,这违背了等价类的定义,怎么办呢?
有些时候,$len(q)≠len(p)+1$ ,比如右图中红点所在的 $len=1$,而他连向的蓝点的 $len=4$,显然 $len(蓝)≠len(红)+1$,所以我们就要使用克隆节点
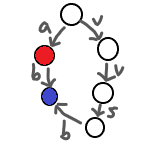
具体来说,因为 $p$ 可以到 $q$ ,所以 $len(q)$ 一定大于等于 $len(p)+1$ ,所以 $len(q)≠len(p)+1$的情况实际为 $len(q)>len(p)+1$ ,意味着还有至少一个比$“longest(p)+s”$ 更长的串属于等价类 $q$ 。而这个更长的串必定不是新串的后缀,因为如果是,那么去掉其最后一个字符得到的字符串必然是旧串的后缀,且其长度大于 $len(p)$ ,因此应该先被跳到。
所以就引出了一个问题,$longest(p)+x$ 是新串的后缀,而同在 $q$ 中有一个更长的 $longest(q)$ 不是新串的后缀,这个时候,我们应该创建一个新的等价类来存放我们的 $longest(p)+1$ ,这个等价类应该有和 $q$ 一样的 $nxt$ 和 $link$ ,且在最后 $q$ 和 $cur$ 的 $link$ 都应该连向它 ,这就是为什么需要一个克隆状态来维护
复杂度证明
我太菜了,给不出完整的证明
尝试感性理解
首先,每一次构造最多产生两个节点,所以节点数量是线性的
在构造的过程中跳 $link$ 时,会将 $cur$ 的 $link$ 设置到最后一次跳的位置,所以每个节点只会被跳一次,时间复杂度也是 $\text{O}(n)$ 的。
空间复杂度上来说,每一次构造最多出现两个节点,所以空间复杂度时 $\text{O}(n\sum)$的,其中 $\sum$ 为字符集的大小,可视作常数,实际上当空间不够时可以牺牲部分时间复杂度使用 $\text{map}$ 存储字符转移
喜闻乐见的板子时间
#include <bits/stdc++.h>
using namespace std;
namespace SAM {
const int N = 1e6 + 114;
const int M = 26;
int cnt, lst;
struct State {
long long len, link;
int nxt[30];
} sam[2 * N];
int sz[2 * N];
void sam_insert(int x) {
int cur = ++cnt;
sam[cnt].len = sam[lst].len + 1;
sz[cnt] = 1;
int p = lst;
while (p != -1 && !sam[p].nxt[x]) {
sam[p].nxt[x] = cur;
p = sam[p].link;
}
if (p == -1) {
sam[cur].link = 0;
} else {
int q = sam[p].nxt[x];
if (sam[p].len + 1 == sam[q].len) {
sam[cur].link = q;
} else {
int clone = ++cnt;
sam[clone].len = sam[p].len + 1;
for (int i = 1; i <= M; i++) {
sam[clone].nxt[i] = sam[q].nxt[i];
}
sam[clone].link = sam[q].link;
while (p != -1 && sam[p].nxt[x] == q) {
sam[p].nxt[x] = clone;
p = sam[p].link;
}
sam[q].link = sam[cur].link = clone;
}
}
lst = cur;
}
void init() {
sam[0].link = -1;
}
void string_insert(string s) {
for (int i = 0; i < s.length(); i++) {
sam_insert(s[i] - 'a' + 1);
}
}
}
using namespace SAM;
vector<int> e[2 * N];
long long ans = 0;
void dfs(int nd) {
for (auto x : e[nd]) {
dfs(x);
sz[nd] += sz[x];
}
if (sz[nd] != 1)
ans = max(ans, sz[nd] * sam[nd].len);
}
int main() {
init();
string x;
cin >> x;
//构造
string_insert(x);
//输出字符转移和后缀链接
for (int i = 0; i <= cnt; i++) {
for(int j=1;j<=26;j++){
if(sam[i].nxt[j]){
cout<<i<<" "<<sam[i].nxt[j]<<" "<<(char)(j+'a'-1)<<endl;
}
}
}
for (int i = 1; i <= cnt; i++) {
cout<<i<<" "<<sam[i].link<<endl;
}
return 0;
}
例题
-
字符串匹配
给你原串 $s_1$ 和一个串 $s_2$,问 $s_1$ 是否包含 $s_2$
较为简单的题目,也可以用SAM做,首先对于 $s_1$ 构建SAM,之后创建指针从 $s_2$ 的头至尾,对于其上的每一个字符,直接大力往对应的字符转移跳即可,由于从 $t_0$ 出发,走字符转移,一定可以走到原串的任意一个子串,所以是正确的
bool dfs(int nd, int curr = 0) { if (curr == s2.length()) { return 1; } else if (sam[nd].nxt[s2[curr] - 'a' + 1]) { dfs(sam[nd].nxt[s2[curr] - 'a' + 1], curr + 1); } else { return 0; } }
- 统计不同子串数量
对于每个节点,其子串数量为 $|longest(t_i)|-|shortest(t_i)|+1$,所以我们只需要求出 $|shortest(t_i)|$ 即可,答案很明显,$shortest(t_i)$ 就是 $longest(link(t_i)) + 1$,直接统计即可
- 统计子串所有出现的位置
考虑对于子串 $x$ 所在的一个状态,出现的位置就是其 $endpos - len(x)$ ,所以我们只需要知道一个状态的 $endpos$ 即可
考虑如何维护第一次出现的endpos,很显然,就是刚插入此子串时的位置,即插入时的 $len(cur)$,
求所有出现的位置,可以考虑将其子树和克隆状态中第一出现的整合起来

