文章	评论	标签
5	0	5

线段树优化建图

日期：2025-08-22浏览：0 编辑

考虑下面的这个问题：

www.luogu.com.cn

显然，这是一道最短路，但是直接建图肯定会 $TLE$，相当于你要把 $l$ 到 $r$ 之内的点全部连一条边，这样单次操作的事件复杂度是 $O(n)$ 的，所以，我们需要考虑一种聪明的方式来优化它。

考虑到这是一堆区间操作，我们可以考虑使用擅长区间操作的线段树来处理。

这是原来的一排点

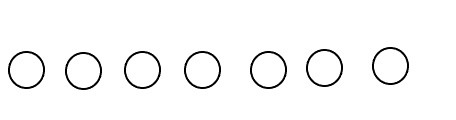
对于优化建图，我有一个暴论，就是所有的优化建图都是通过建造辅助点来对一个区间连边的。

首先来考虑操作 $2$

我们考虑以这排节点为叶子，建一颗外向线段树：

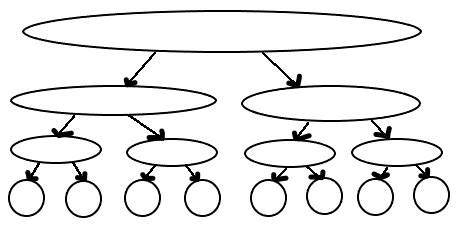
现在，如果我们朝一个父节点连边，那么相当于朝这个树子树内的所有叶子连一条边了。

好的，接下来处理操作 $3$，同理，如果我们要让边连出去的话，可以建一颗内向树，这样，从父节点连一条出边，就相当于它的所有子树都连了一条出边，最后，整棵树会形成这样的结构：

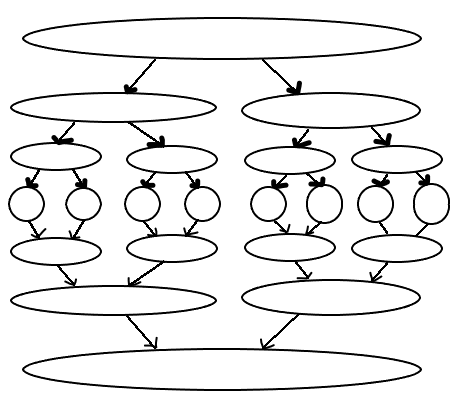
现在，图就建完了，如果我们需要连边，也很简单，像线段树那样就行了。

比如我们要从第一个点连像区间[4,7]，我们只需要这样子连

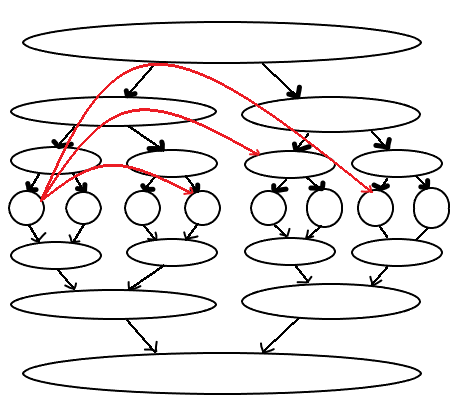
是不是非常简单呢！

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 110000;
int n,m,ds,s;
struct edge{
    int v;
    ll w;
};
vector<edge> e[10*N];
struct xds{
    int dir = 1;
    struct node{
        int l,r;
        int lson,rson;
    }a[N*4];
    int build(int l,int r){//建树
        if(l == r){//如果这个区间只有一个点，那么就连到那个点
            a[l].l = l,a[l].r = r;//记得这里要更新！否则 WA on test 5#
            return l;
        }
        int wAi = ++ds;
        int mid = (l+r)/2;
        a[wAi].l = l,a[wAi].r = r;
        a[wAi].lson = build(l,mid),a[wAi].rson = build(mid+1,r);//基本的建树
        if(dir){//方向判断是外向树还是内向树
            e[wAi].push_back({a[wAi].lson,0});
            e[wAi].push_back({a[wAi].rson,0});
        }else{
            e[a[wAi].lson].push_back({wAi,0});
            e[a[wAi].rson].push_back({wAi,0});
        }
        return wAi;
    }
    void addfrom(int u,int v,ll w,int l,int r){//从点 u 连向区间 [l,r]
        if(l<=a[v].l && a[v].r<=r){
            e[u].push_back({v,w});
            return;
        }else if(l>a[v].r || r<a[v].l){
            return;
        }else{
            addfrom(u,a[v].lson,w,l,r);
            addfrom(u,a[v].rson,w,l,r);
            return;
        }
    }
    void addto(int u,int v,ll w,int l,int r){//从区间 [l,r] 连向点 u
        if(l<=a[v].l && a[v].r<=r){
            e[v].push_back({u,w});
            return;
        }else if(l>a[v].r || r<a[v].l){
            return;
        }else{
            addto(u,a[v].lson,w,l,r);
            addto(u,a[v].rson,w,l,r);
            return;
        }
    }
}out,in;
vector<long long> dist(10*N, LONG_LONG_MAX); 
void dij() {//最短路板子
	priority_queue<pair<long long, int>, vector<pair<long long, int>>, greater<pair<long long, int>>> pq;
	pq.push({0, s});
	dist[s] = 0;
	while (!pq.empty()) {
		long long d = pq.top().first;
		int u = pq.top().second;
		pq.pop();

		if (d > dist[u])
			continue;

		for (auto edge : e[u]) {
			int v = edge.v;
			long long w = edge.w;
			if (dist[u] + w < dist[v]) {
				dist[v] = dist[u] + w;
				pq.push({dist[v], v});
			}
		}
	}
	return ;
}
int main() {
    cin>>n>>m>>s;
    ds = n;
    int rt_out = out.build(1,n);
    in.dir = 0;
    int rt_in = in.build(1,n);
    for(int i=1;i<=m;i++){
        int opt;
        cin>>opt;
        if(opt==1){
            int u,w,v;
            cin>>u>>v>>w;
            e[u].push_back({v,w});//由于我们直接以节点为叶子节点，所以可以直接连边
        }else if(opt==2){
            int u,w,l,r;
            cin>>u>>l>>r>>w;
            out.addfrom(u,rt_out,w,l,r);
        }else{
            int u,w,l,r;
            cin>>u>>l>>r>>w;
            in.addto(u,rt_in,w,l,r);
        }
    }
    dij();
    for(int i=1;i<=n;i++){
        cout<<((dist[i]==LONG_LONG_MAX)?-1:dist[i])<<" ";
    }
	return 0;
}