优化建图是一种图论中的辅助方法，通过建辅助点的方法将图优化，通常，这可以大幅度减少算法的时间复杂度和空间复杂度。

例题

檀香梅

题解

这道题如果使用传统的直接建图，则一共有 $O(n^2)$条边，在 TLE 之前就已经 MLE 了，所以我们考虑到使用其他方法。

考虑到这道题由于有 $m$ 条任意边，所以卡掉了 DAG 上跑 dp 的方法。

此时发现 $x_i≤x_j$ 且 $y_i≤y_j$ 是偏序问题，考虑使用cdq分治优化。

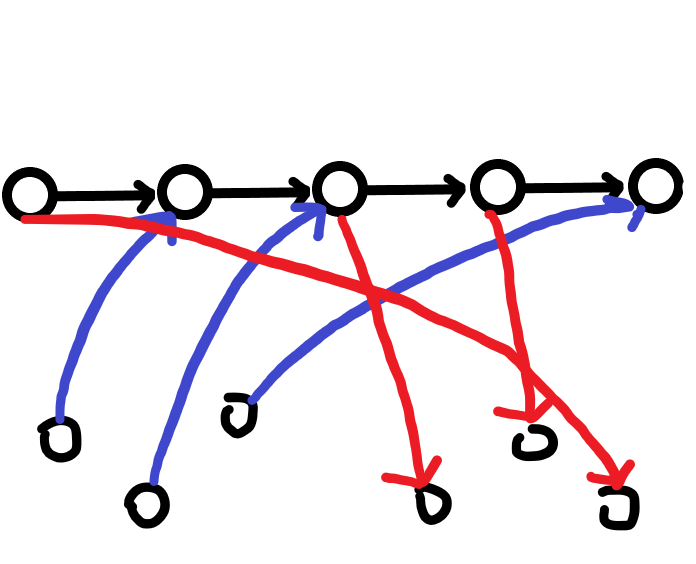
先对与每个点按 $x$ 从大到小排序，然后分治。

分治时，对于区间 $(l,r)$ ，对于所有 $y_i (l≤i≤r)$ 建一个点，且将所有点和建的下一个点相连

之后对于所有的 $l≤i≤mid$ 将 $i$ 向 $y_i$ 的对应辅助点连一条边，

对于 $mid+1≤i≤r$ ，将 $y_i$ 对应的点向 $i$ 连一条边

这样子一共会有 $logn$ 个点和 $logn$ 条边，时间复杂度的瓶颈为最短路 $O(mlogm) = O(nlog^3n)$

#include <bits/stdc++.h>
#define st(a) ((a) * 2 - 1)
#define ed(a) ((a) * 2)

using namespace std;

int n, m;
int ds = 0;

struct node {
	long long x, y;
} a[410000];
map<long long, int> b;
set<long long> fz;
struct edge {
	int v;
	long long w;
};
vector<edge> e[2100000];
vector<long long> dist(2100000, LONG_LONG_MAX); 

bool cmp(node x, node y) {
	if (x.x == y.x) {
		return x.y < y.y;
	} else {
		return x.x < y.x;
	}
}

void solve(int l, int r) {
	if (l >= r) {
		return;
	}
	int mid = (l + r) / 2;
	solve(l, mid), solve(mid + 1, r);
	fz.clear(), b.clear();
	for (int i = l; i <= r; i++) {
		fz.insert(a[i].y);
	}
	int num = 0;
	long long lstnum = 0;
	for (auto xx : fz) {
		num++;
		ds++;
		if (num > 1) {
			e[ds - 1].push_back({ds, xx-lstnum});
		}
		lstnum = xx;
		b[xx] = ds;
	}
	for (int i = l; i <= mid; i++) {
		e[i].push_back({b[a[i].y], 0});
	}
	for (int i = mid + 1; i <= r; i++) {
		e[b[a[i].y]].push_back({i, 0});
	}
}

void dij() {
	priority_queue<pair<long long, int>, vector<pair<long long, int>>, greater<pair<long long, int>>> pq;
	pq.push({0, 1});
	dist[1] = 0;
	while (!pq.empty()) {
		long long d = pq.top().first;
		int u = pq.top().second;
		pq.pop();

		if (d > dist[u])
			continue;

		for (auto edge : e[u]) {
			int v = edge.v;
			long long w = edge.w;
			if (dist[u] + w < dist[v]) {
				dist[v] = dist[u] + w;
				pq.push({dist[v], v});
			}
		}
	}
	return ;
}

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	// freopen("blossom.in","r",stdin);
	// freopen("blossom.out","w",stdout);
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		long long x, y;
		cin >> x >> y;
		a[i].x = x;
		a[i].y = y;
	}
	ds = n;
	solve(1, n);
	for (int i = 1; i <= m; i++) {
		int u, v;
		long long w;
		cin >> u >> v >> w;
		e[u].push_back({v, w});
	}
	// cerr<<(double)clock()/CLOCKS_PER_SEC<<endl;
	dij();
	for(int i=1;i<=n;i++){
		if(dist[i]==LONG_LONG_MAX)cout<<-1<<" ";
		else cout<<dist[i]<<" ";
	}
	// int mem = 0;
	// for (int i = 1; i <= ds; i++) {
		// mem+=sizeof(e[i]);
	// }
	cerr<<(double)clock()/CLOCKS_PER_SEC<<endl;
	return 0;
}